《深度学习入门》学习笔记(一)
本文最后更新于:2025年10月20日 下午
《深度学习入门》学习笔记(一)
第一章 Python入门
第一次接触python是在我大一的时候,那时候python很火,同时火的还有大数据、云计算、人工智能。现在,大数据,云计算的呼声渐渐褪去,人工智能却还是一如既往的火热。同时,也让python成为了最具有人气的编程语言。
1.1 什么是Python
什么是python?python是一门简单、易读、易记的编程语言,而且是开源的,可以免费使用。上面这句话来源于我手头的一本书《深度学习入门》。对于这句话,我还是挺想吐槽的。我自学python也有将近一年多了,简单是入门简单,易读是小代码段易读,在大量代码体中,python的缩进排版真的很难去分清代码块。它不像C语言一样有一个大括号括起来,在庞大的代码体中可以一一对应。而python呢?是以缩进的形式,难以去形成一一对应关系。易记是易记,因为库是真的多,被别人封装好的库你直接去调用,根本不用去思考它的原理,只要会用你就能完成你的任务。所以,造成了入门简单,精通很难。以上便是我对python的理解和评价,下面进入正题。
1.2 Python的安装
想使用python就必须要安装python的开发环境,我们通常使用的是在电脑(windows或linux)上。因为手机的安卓是基于linux内核的开发的,所以在一些特定的软件上也是可以做python的开发。如Termux,QPython3H等app,都可以在手机上使用和开发python的相关项目。
具体安装步骤请百度,有很多图文教程,我在这里就不再次描述了。
1.2.1 Python的版本
Python有python2和python3两个版本,现阶段python2基本上已经被遗弃了,但还是有不少的人去使用。很奇怪的是python跟别的编程语言不一样。它对于版本适配上没有别的编程语言好。例如python2的一些语法跟python3就不一样。你用python3写的代码就不能被python2执行,没有向后兼容性。所以,还是用最新的版本python3来学习深度学习吧。
1.2.2 使用的外部库
前面我说过,python很简单,易记是因为它有一个极其庞大的外部库。许许多多的大佬将一些功能封装成外部库,我们只需要调用它留给我们的接口就能很快的实现某种功能。所以,如果你想精通python,就不要过多的使用外部库,尽可能自己去实现相关的一些功能。
关于外部库的安装,我们通常通过pip这个包管理器去安装。使用方式就是在命令窗口输入
pip install 你要安装的外部库名
然后等待安装即可。
例如安装我们要使用的NumPy库、Matplotlib库等,如下:
pip install numpy,matplotlib
回车即可安装。
1.3 Python解释器
python安装后,需要先确认一下你的python的版本是否正确。打开命令提示符窗口,输入:
python --version
即可看到你安装的python版本号。
什么是解析器?
解析器就像是两个人对话一样,你一句,我一句的对话模式。例如我问你1+1=?,然后你会回答我等于2.python就是这样,不需要编译,就可以直接跟你互动。这就是对话式(交互式)的编程。
如:
>>> 1+1
2
1.3.1 算术计算
算术计算加法和减法可以直接写数学算术计算进行,如下:
>>> 1+1 //+是加法
2
>>> 2-1 //-是减法
1
>>> 4/2 // /是除法
2.0
>>> 2*2 // *是乘法
4
>>> 2**2 // **是乘方
4
1.3.2 数据类型
编程里的各种数据都是有类型的,有利于对数据进行分类。但数据类型这一概念在python里我觉得是一个坑。因为你不用像C语言那样提前定义好数据类型,而是python自己识别并定义数据类型。所以,在写python项目时,有时候会因为数据类型出现一些bug,但你有时候还真无法分辨python给你定义的变量分配了什么数据类型,往往需要强制转换变成自己想要的数据类型。
数据类型有哪些呢?
常用的数据类型有:整数型,浮点型(小数),字符型和字符串型。
你如何去判断你定义的变量或者常量的数据类型呢?
在python中提供了type()函数来查看数据类型
例如:
>>> type(10)
<class 'int'>
>>> type(2.66)
<class 'float'>
>>> type("hello")
<class 'str'>
>>> type('a')
<class 'str'>
1.3.3 变量
变量,看名字就可以理解,是一个变化的量。本质上不是特定的一个数,为了方便理解,我通常把它比作成一个盒子,这个盒子是有属性的,也就是数据类型。也就是符合放入盒子的条件(数据类型)的数据才能放入其中。
例如:
>>> x = 10
>>> print(x)
10
变量也是可以进行数学运算的,例如:
>>> x = x + 1
>>> print(x)
11
print是python的输出打印函数,就是把数据呈现在你的电脑屏幕上的函数。
1.3.4 列表
在编程语言中,除了我们用的单一数值,往往还需要汇总的数据。这时候就需要引入列表(数组)的概念了。如:
>>> a = [1,2,3,4,5] #生成列表
>>> print(a) #打印列表
[1, 2, 3, 4, 5]
除此之外还要对列表有一系列数据操作,如:
>>> len(a) #获取列表长度
5
>>> a[0] #访问列表的第一个元素
1
>>> a[4] #访问列表最后一个元素
5
>>> a[4] = 100 # 对列表最后一个元素重新赋值
>>> print(a)
[1, 2, 3, 4, 100]
要注意的是在编程语言中,开始都是以0为开始,并不是1。
这些数据处理往往还是不够,我们还要引入“数据切片”。这个词也是我自己起的(好像有些书也是这么写的),就像切片一样,切下我们想要的数据片段。用法如下:
>>> print(a)
[1, 2, 3, 4, 100]
>>> a[0:2] #注意,该切片从0到2,但并不包括2。
[1, 2]
>>> a[1:] #从1开始往后所有
[2, 3, 4, 100]
>>> a[:3] #从0开始到3,不包括3
[1, 2, 3]
>>> a[:-1] # 从0开始到最后一个元素的前一个元素
[1, 2, 3, 4]
>>> a[:-2] # 同上,最后一个元素的前两个元素
[1, 2, 3]
1.3.5 字典
字典,就像字典一样,是一种索引的方法。像新华字典一样对应的单词与对应的含义关联起来。例如:
>>> me = {"我的名字":"连思鑫"}
>>> me["我的名字"]
'连思鑫'
1.3.6 布尔型
布尔型,这是我们学习深度学习最常用的一个概念。bool型是只有两种状态:True和False。后面要学的感知机就要用到大量的bool型。
而对于bool型的运算包括:and、or、not这些逻辑运算符。如果涉及到数值则有:+、-、*、/等。
实例如下:
>>> hungry = True # 饿了? 饿
>>> sleepy = False #困了? 不困
>>> type(hungry)
<class 'bool'>
>>> not hungry # 不饿
False
>>> hungry and sleepy #饿并且困
False
>>> hungry or sleepy #饿或者困
True
1.3.7 if语句
if语句是判断语句,现在的流行语言中都有它的身影。无论C,C++,Java、JavaScript等都有if语句,用法也都大相径庭。如下:
>>> hungry = True
>>> if hungry:
print("饿了")
饿了
需要注意的地方,python的代码块格式是通过缩进的形式(4个空格)。个人不太喜欢这种形式,不容易看,但是没办法,谁让咱没能力开发编程语言呢?
1.3.8 for语句
for语句是循环语句,同if语句一样,各大主流语言也都有它的身影,且用法大相径庭。 例如:
>>> for i in [1,2,3]:
print(i)
1
2
3
该语句的意思是循环打印列表元素。for语法通常用for…in…:的语句结构,i是用来存放每次循环数据的盒子(变量)。
1.3.9 函数
所有的编程语言都有函数的概念,为了方便对数据的处理,所以我们把一连串的处理定义成函数。即如下的打印hello的函数:
>>> def hello():
... print("hello")
...
>>> hello()
hello
hello()就是对该函数进行调用,函数除了可以被调用,还可以进行传参。如下:
>>> def hello(s): # s是定义的变量
... print("hello" + s)
...
>>> hello("连思鑫")
hello连思鑫
+号在python中除了是用于算术运算之外,还可以用于拼接字符串。二者的区别在于数据类型的不同,+号的用法或体现的功能不同。
1.4 Python脚本文件
python除了解释器编程外,也支持保存成脚本文件。因为以对话的形式不能更好的去保留对话内容,所以人们发明了纸张。同样的,这个脚本文件的存在就像是一张纸,你可以把想对python说的话同一写在纸上,然后python按你说的做。
emmmmm…我喜欢计算机的原因也在其中。计算机就像是你忠实的奴仆一样,只要你说的它能听懂,它就会毫无置疑的去做。就像皇帝命令臣子,而这个臣子不会反抗且非常听话。在linux系统下,你要是看系统不顺眼,完全可以命令它自杀,如:
rm -rf /
祝你好运!
1.4.1 保存为文件
如何保存为python的脚本文件呢?其实有很多很多办法,最简单的就是用记事本,写一些python代码,然后把文件的后缀改成.py即可。
如何运行它呢?不管是windows还是linux只要安装好python的环境,在终端输入
python xxx.py
即可运行你写的脚本文件。
1.4.2 类
什么是类?有说的好,叫物以类聚,人以群分。这个类便是我们对数据和处理数据的方法集结在一起的共同体(或者叫它类型)。如我们前面用到的int和str这些数据类型,它们是python内置的数据类型,是python开发者定义和设计的类。而我们学好类这一概念,便可以自己去创造定义一个类。
各大语言中也都有类的概念,类包含了方法和属性,其中的方法就是我们上面说的函数的概念。在python中类的定义格式如下:
class 类名:
def __init__(self,参数,...): #这是构造函数(可以把它理解成类入口,或者默认函数)
函数体(方法体)
def 方法名1(self,参数,...):
函数体
def 方法名2(self,参数,...):
函数体
.....
关于__init__方法,这是一种初始化的方法,实际只被调用一次(在生成实例时)。而self是用来传参的变量。示例如下
class Man:
def __init__(self, name):
self.name = name
print("我进入了这个类喽!")
def hello(self):
print("hello"+self.name)
def goodbye(self):
print("再见"+self.name)
m = Man("连思鑫")
m.hello()
m.goodbye()
运行结果如图:
讲解:这里我们定义了一个新的类,名字叫Man。在上面的代码中,我们用Man类生成类实例(对象)m。 一开始,类Man的构造函数接受到了name,这个时候说明我的名字已经进入到了Man类中。然后我的名字便随着实例变量self.name漂流到下一个方法hello中,这时你就能理解self是干什么用的了。实例变量是储存在各个实例中的变量,可以通过self加属性名的方式来生成或访问实例变量。
1.5 NumPy库
在深度学习中,经常出现数组和矩阵的运算。我们大家看到的图片,电影,游戏等,其实都是1010的二进制以多维数组或矩阵组合而成。就拿图像来说,图像就是由许许多多的像素以矩阵的形式排列而成,每个像素又是一个数组,其中包含类RGB等色彩属性,明暗属性等。所以,我们学习深度学习就离不开数组和矩阵的运算,而数组和矩阵的计算常用这节要学的外部库Numpy。Numpy的优异之处在于它提供了许多有关于数组运算的便捷方法,如numpy.array。具体用法后面会详细的说。
1.5.1 导入NumPy
Numpy是python的外部库,所以需要先下载这个外部库才能使用。我们可以用pip包管理器进行下载,如何使用上面章节已经讲述,我就不再赘述。
下载好之后并不是就能直接使用,我们需要把它导入到我们的项目中,导入方法如下:
import numpy as np # as np的意思是把numpy导入作为np来使用。
1.5.2 生成NumPy数组
导入成功后,我们便要对它操作使用,要生成我们所需要的数组,需要调用numpy的array()方法。如下:
>>> import numpy as np
>>> x = np.array([1,2,3,4,5])
>>> print(x)
[1 2 3 4 5]
>>> type(x)
<class 'numpy.ndarray'>
1.5.3 NumPy的算术运算
关于运算,不知道怎么说,还是举例说明吧。举例如下:
>>> x = np.array([1.0,2.0,3.0])
>>> y = np.array([2.0,3.0,4.0])
>>> x + y #对应元素相加/减/乘/除
array([3., 5., 7.])
>>> x - y
array([-1., -1., -1.])
>>> x * y
array([ 2., 6., 12.])
>>> x / y
array([0.5 , 0.66666667, 0.75 ])
关于数组的计算方式,参考线性代数。
注:数组x和数组y的元素个数是相同的,所以可以进行算术运算。如果元素个数不同,在进行算术运算时python就会报错。
Numpy不仅可以进行对应元素的算术运算,还支持各元素之间跟标量之间运算,如:
>>> x = np.array([1.0,2.0,3.0])
>>> x / 2.0
array([0.5, 1. , 1.5])
1.5.4 NumPy的N维数组
上一节演示的是一维数组,Numpy不仅可以创建一维数组,还可以创建多维数组。如二维数组就是线代里的矩阵了。例:
>>> A = np.array([[1,2],[3,4]])
>>> print(A)
[[1 2]
[3 4]]
>>> A.shape
(2, 2)
>>> A.dtype
dtype('int64')
这里我们生成了一个2x2的矩阵A。另外,矩阵A的形状可以通过shape来看,上面表示的意思就是2行2列的数组。而数据元素的数据类型可以通过dtype来查看。
接下来我们看一下多维数组的算术运算。如下:
>>> import numpy as np
>>> A = np.array([[1,2],[3,4]])
>>> B = np.array([[3,0],[0,6]])
>>> A + B
array([[ 4, 2],
[ 3, 10]])
>>> A * B
array([[ 3, 0],
[ 0, 24]])
和一维数组运算一样,要遵循元素对应的法则,不然容易报错。同时也支持通过标量(单一数值)进行矩阵的算术运算,也就是后面要说的广播。如下:
>>> print(A)
[[1 2]
[3 4]]
>>> A * 10
array([[10, 20],
[30, 40]])
注解:在数学领域中,一维数组的概念在数学中是以向量的形式存在的,二维数组是矩阵。而线代里统一把这些称之为张量或多维数组。
1.5.5 广播
在Numpy中,形状不同的数组之间也是可以进行运算。之前咱们的例子中,在一个2x2的矩阵A和标量10之间进行了乘法运算。在运算过程中,10被拓展成2x2的形状依次和A矩阵的每个元素进行运算。而这个过程称之为广播。
关于广播更通俗的解释(个人解释):广播就像农村里的大喇叭,它喊出来的信息大家伙都能接受到听到。也就是这个信息传递到每一个人,每个人在对其做相应的处理。
例:
>>> A = np.array([[1,2],[3,4]])
>>> B = np.array([10,20])
>>> A * B
array([[10, 40],
[30, 80]])
在这个运算中,一维数组被展开成和二维数组相同的形状(注意,只是形状相同,而不是变成了二维数组),与矩阵A进行运算(元素对应)。
综上所述,Numpy有广播的功能,所以可以对不同形状的数组之间进行运算。
1.5.6 访问元素
Numpy数组的元素访问和列表相似,都是通过下标进行访问。如下:
>>> x = np.array([[1,2],[3,4]])
>>> print(x)
[[1 2]
[3 4]]
>>> x[0] #第0行的所有元素
array([1, 2])
>>> x[0][1] #第0行第2个元素(编程语言是从0开始算起的)
2
也可以用for循环历遍各个元素。如下:
>>> for i in x:
... print(i)
...
[1 2]
[3 4]
除了上面说的索引操作,Numpy还支持用数组的形式访问各个元素。
>>> import numpy as np
>>> x = np.array([[11,22],[33,44],[55,66]])
>>> print(x)
[[11 22]
[33 44]
[55 66]]
>>> x = x.flatten() #将x转换成一维数组
>>> print(x)
[11 22 33 44 55 66]
>>> x[np.array([1,3,5])] #以数组的形式访问x数组的各项元素(1,3,5)
array([22, 44, 66])
运用这种方法可以设定一定条件,满足条件的可以从x数组中抽出自己想要的结果。
例如提取x中大于20的元素,可以用如下方式实现:
>>> print(x)
[11 22 33 44 55 66]
>>> x > 20
array([False, True, True, True, True, True])
>>> x[x>20]
array([22, 33, 44, 55, 66])
对Numpy数组使用不等号运算符等得到的结果是个布尔型的数组,在跟据满足ture条件的元素取出显示。
注解:Numpy好用的地方在于它有许多处理是用C/C++实现的,python在业内有胶水语言的称号,可以作为中间人,复合使用是效率最大化。相较于静态类型语言(C/C++),python的运算速度就很慢。
1.6 Matplotlib库
有了各种数据的操作往往还不够,我们在学数学时有个数形结合的思想。想要更好的理解这些数据的规律、形式、意义等,我们就不得不要对其进行可视化操作。而Matplotlib库便可以轻松的绘制图形使数据可视化。
我之前还打算用Matplotlib库结合Numpy库来总结和学习高数的内容,算是半途而废了,最后我会展示我之前所做的半成品。
1.6.1 绘制简单图形
matplotlib库的pyplot模块可以绘制图形,直接举例:
import numpy as np
import matplotlib.pyplot as plt
#生成数据
x = np.arange(0, 6, 0.1) # 以0.1为单位,生成0到6的数据
y = np.sin(x)
#绘图
plt.plot(x,y)
plt.show()
这里我们使用了Numoy库的arange方法生成了一个[0,0.1,0.2…5.9]的数据,并设它为x。对x的数据逐一应用Numpy的sin函数得到的数据定义为y。最后将x,y的值传递给plt.plot方法,然后绘图。通过plt.show()显示图像。如下图:
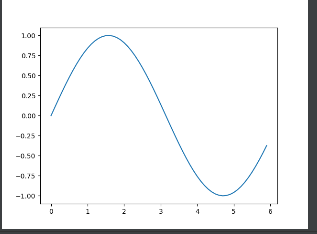
1.6.2 pyplot的功能
在刚才的sin函数的图形中,我们尝试追加cos函数的图形,并尝试使用pyplot的添加标题和x轴标签名等其他功能。
import numpy as np
import matplotlib.pyplot as plt
#生成数据
x = np.arange(0, 6, 0.1) # 以0.1为单位,生成0到6的数据
y1 = np.sin(x)
y2 = np.cos(x)
# 绘图
plt.plot(x, y1, label="sin")
plt.plot(x, y2, linestyle="--", label="cos") # 用虚线表示
plt.xlabel("x")
plt.ylabel("y")
plt.title("sin & cos")
plt.legend()
plt.show()
展示结果如下:
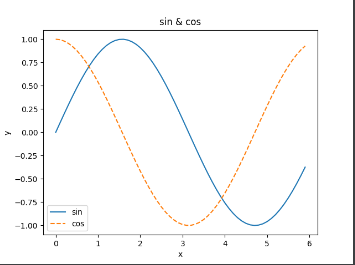
1.6.3 显示图像
pyplot 中还提供了用于显示图像的方法 imshow()。另外,可以使用matplotlib.image模块的imread()方法读入图像。下面我们来看一个例子。
import matplotlib.pyplot as plt
from matplotlib.image import imread
img = imread('001.jpg') # 读入图像(设定合适的路径!)
plt.imshow(img)
plt.show()
执行结果如下:
这里,我们假定图像lena.png在当前目录下。大家可以根据自己的环境,可能需要变更文件名或文件路径。将图像的路径 '001.jpg’改为你电脑上图片所在目录即可正确运行。
1.6.4 半成品项目
下面是我很久很久以前自学python时的想法,想结合高数用python去理解数学。
#第一章:集合与常用逻辑
##集合是只具有某种特定性质的事物的总体。组成这个集合的事物称之为该集合的元素。
#一个集合,若它的元素是有限的话,我们称之为有限集。反之不是有限的我们称之为无限集。
import numpy as np
import math
#声明两个空集合,命名为A,B。
A = {} #A集合
B = {} #B集合
#集合之间的关系:
#相等:集合A和集合B中的所有元素都相同
A = {1,2,3}
B = {1,3,2}
if A==B:
print("A集合与B集合相等!")
else:
print("A集合不等于B集合!")
#子集:集合A中任意一个元素都是集合B中的元素
A = {1,2,3}
B = {1,2,3,4,5}
result = A <= B
if result:
print("A是B的子集!")
else:
print("A不是B的子集!")
#真子集:集合A中任意一个元素都是集合B中的元素,且集合B中至少有一个元素不是集合A中的元素
A = {1,2,3}
B = {1,2,3}
result = A < B
if result:
print("A是B的真子集!")
else:
print("A不是B的真子集!")
#空集:是任何集合的子集,是任何非空集合的真子集
A = {}
B = {}
#并集:由集合A和集合B共同组成的集合叫并集(A并B)
A = {1,2,3,4}
B = {5,6,7,8,9}
result = A | B
print(result)
#交集:集合A和B共同拥有的元素构成的集合
A = {1,2,3,4}
B = {3,4,5,6}
result = A & B
print(result)
#补集与全集
U = {1,2,3,4,5,6,7,8,9} #全集
A = {1,2,3,4,5}
result = U - A #补集
print(result)
'''
函数介绍:numpy库中的arange方法生成的是左开右闭的区间。
'''
#开区间
x = np.arange(1+1,10)
print("这是(1,10)的开区间:" + str(x))
#闭区间
x = np.arange(1,10+1)
print("这是[1,10]的闭区间:" + str(x))
'''
无穷数的介绍:在python中其实也是可以表示正负无穷数的。
在此,我们使用float('inf')来表示正无穷数,float('inf')来表示负无穷数。
如何检测无穷数呢?我们用到math库的isinf()方法来判断
'''
# 无穷大
x = float('inf') #用于表示无穷大
y = 100000000000000000
print(math.isinf(x))
print(math.isinf(y))
#逻辑门(与,或,非)
class Logic:
def __init__(self,x):
self.x = x
def AND(self): #与门运算
w = np.array([0.5,0.5])
t = 0.7
sum = np.sum(self.x*w)-t
print(str(self.x[0]) + "与" + str(self.x[1]) + "为:")
if sum <= 0:
print(0)
elif sum > 0:
print(1)
def OR(self): #或门运算
w = np.array([0.7, 0.7])
t = 0.5
sum = np.sum(self.x * w) - t
print(str(self.x[0]) + "或" + str(self.x[1]) + "为:")
if sum <= 0:
print(0)
elif sum > 0:
print(1)
s = np.array([[1,0],[0,1],[0,0],[1,1]])
for x in s:
# 实例化对象
logic = Logic(x)
#与门
logic.AND()
#或门
logic.OR()
# 第二章:函数
import numpy as np # 计算
import math
import matplotlib.pyplot as plt # 画图
import sympy as sp # 函数库
import interval as iv # 区间库
# 函数 :由两个非空集合相互对应的一种表示(可一对一,多对一)
x = sp.symbols("x") # 定义未知数x,x为非空集合中的一个未知元素。
y = sp.solve(x, x) # 函数关系式,该方法是在函数等用0的时候参与运算求解,得到的结果为数组。
print(y)
x = np.arange(-5.0, 5.0, 0.1) # 定义x的区间和表示单位
y = x # 函数体
plt.plot(x, y)
plt.ylim(-10, 10) # 定义y的区间
plt.show()
# 函数相等:如果两个函数定义域相同,对应关系完全一致,称这两个函数相等。
x1 = np.arange(-5.0, 5.0, 0.1)
x2 = np.arange(-5.0, 5.0, 0.1)
y1 = x1
y2 = pow(pow(x2, 2), 0.5) # y2 = x2的平方开算术平方根,pow是算平方的内置方法
plt.plot(x1, y1)
plt.plot(x2, y2, linestyle="--")
plt.ylim(-10, 10)
plt.show() # 如图所示,不是相等函数。
# 函数奇偶性:如上图可看出,y(-x)=-y(x)是奇函数,y(-x)=y(x)是偶函数
# 分段函数: 给定不同的区间有不同的对应关系的函数
x1 = np.arange(-5.0, 0.0, 0.1)
x2 = np.arange(0.0, 5.0, 0.1)
y1 = x1
y2 = pow(x2, 2)
plt.plot(x1, y1)
plt.plot(x2, y2, linestyle="--")
plt.ylim(-10, 10)
plt.show() # 如图是分段函数
# 一次函数:又叫线性函数。y=kx+b(k!=0)
x = np.arange(-5.0, 5.0, 0.1)
y = 2 * x + 2
plt.plot(x, y)
plt.ylim(-10, 10)
plt.show() # 如图,是一条直线,k是直线的斜率,b是y轴上的截距。
# 二次函数:非线性函数,抛物线。
x = np.arange(-5.0, 5.0, 0.1)
y = 2 * x ** 2 + 3 * x + 2
plt.plot(x, y)
plt.ylim(-10, 10)
plt.show()
# 指数函数:非线性
x = np.arange(-1, 3, 0.1)
y = -2 ** x
plt.plot(x, y)
plt.ylim(-2, 25)
plt.show()
# 三角函数
# sin函数
x = np.arange(-5,5,0.1)
y = np.sin(x)
plt.plot(x,y)
plt.ylim(-2,2)
plt.show()
#cos函数图像
x = np.arange(-5,5,0.1)
y = np.cos(x)
plt.plot(x,y)
plt.ylim(-2,2)
plt.show()
###
# 动画演示玫瑰线的绘画过程
###
from matplotlib import pyplot as plt
import numpy as np
import math
i = np.linspace(0,2*math.pi,500)
theta=5*np.sin(3*i)
plt.title('p=5*sin(3*i)',color='r')
i_list=[]
theta_list=[]
for (i_tmp,theta_tmp) in zip(i,theta):
i_list.append(i_tmp)
theta_list.append(theta_tmp)
#去除负值,使得动画更顺畅
if(theta_tmp>=0):
plt.plot(i_list,theta_list)
plt.pause(0.01)
plt.axes(polar=True)
plt.ylim(0,5)
#保存动画
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
# 生成图例
fig = plt.figure(figsize=(5,5))
ax = plt.subplot(projection='polar')
# 绘制动态函数的变量
x = np.linspace(0, 2*np.pi, 500)
# 实例化线条
line, = ax.plot([], [], color='r')
r,theta=[],[]
def init():
# 设置y轴的范围
ax.set_ylim(0, 5)
return line
# 更新函数,n是动态变量
def update(n):
# 更新数据
theta.append(n)
r.append(5*np.sin(3*n))
line.set_xdata(theta)
line.set_ydata(r)
return line
# frames在调用update函数时,会将frames后面的数据作为实参传递给“n”
# interval更新频率,单位ms
ani = animation.FuncAnimation(fig, update,frames=x,init_func=init,interval=10)
ani.save('sin.gif',writer='pillow')
##
# 玫瑰线
##
from matplotlib import pyplot as plt
import numpy as np
import math
i = np.linspace(-2*math.pi,2*math.pi,500)
theta=5*np.sin(3*i)
plt.subplot(221,projection='polar')
plt.plot(i,theta)
plt.title('p=5*sin(3*i)',color='r')
theta=5*np.sin(2*i)
plt.subplot(222,projection='polar')
plt.plot(i,theta)
plt.title('p=5*sin(2*i)',color='r')
theta=5*np.sin(3/2*i)
plt.subplot(223,projection='polar')
plt.plot(i,theta)
plt.title('p=5*sin(3/2i)',color='r')
theta=5*np.sin(1*i)
plt.subplot(224,projection='polar',title='p=5*sin(3*i)')
plt.plot(i,theta)
plt.title('p=5*sin(1*i)',color='r')
plt.show()
总结
本章重点介绍了实现深度学习(神经网络)所需的编程知识,以为学习深度学习做好准备。从下一章开始,我们将通过使用Python实际运行代码,逐步了解深度学习。
(本章完结)!